Friday, November 28, 2008
Hi I'm Ben
Here's a little math fun. Mr. K showed us this video back when I was in his Grade 11 Precalc Class and it was really funny. Good job on the posts so far and have fun this semesters
http://www.youtube.com/watch?v=avDxWrdbjws&feature=related
Wednesday, November 26, 2008
Paul's Blog

1. First we labelled the triangle.
2. Second we found angle DEF (70 degrees) because it is the exterior angle (the measure of an exterior angle is equal to the sum of the interior opposite angles) to angle ADE.
3. Then we found out that x= 100 degrees because it is the exterior angle to andgle CDE.
4. And finally we found y=60 be cause x is exterior to angle BAC, therefore you already knew that one angle in triangle ABC was fourty and 40 + y = x whereas x=100, therefore y= 60.
After that problem was solved we went on to another set of problems where the reflexive property was required. The reflexive property means that something is identical to itself.
This triangle is congruent due to the Congruent Triangles Law (SSS).
After that the class went over Circle Geometry - Investigation 2.
We were shown methods of finding the middle of the circle and then he assigned us Investigation 3 for homework.
Next blogger, which was randomly selected, is Stephanie.
Tuesday, November 25, 2008
I will be your host for tonite's Math meal

Check out this picture this is the same one from the white board Mr.Kuros kindly showed us and we instinctively learned like students what the meaning of this mis mash is about!
****too explain in detail.... without too many words ill put up pictures but in groups of 3 for the definitions*****
So check out what a line Segment, a chord and a Diameter are...

How about what the heck is a Secant, Tangent, or ooo a Radius!
 Just because I like you Ladies and Gentleman I'll define to you what the heck is are Major and Minor Arcs, what is meant by being bounded by something, what's a Sector and what an INSCRIBED ANGLE is.... although this will be the last circle for tonite
Just because I like you Ladies and Gentleman I'll define to you what the heck is are Major and Minor Arcs, what is meant by being bounded by something, what's a Sector and what an INSCRIBED ANGLE is.... although this will be the last circle for tonite(Aww... too bad actually I'm actually getting tired of making these circles)

Well to end off this night peoples Im going to say there is this assignment similar to that of today's work where it covers all what I summarized for you Ladies and Gents.
Oh yeah Exercise 30 is on this material also.
I hope this meets Textbook/Mr . Kuro's standards just kidding but I do wish that it hasn't been a waste of your time to read this peoples. '
Give yourselves a hand for taking your time to learn.
And to on a final note Gambete Mina (work hard everyone) '''
*bows and waves*
nExT scriber is D'Lan
*clap clap clap and passes baton while running away*
Sunday, November 23, 2008
reflection
Analytic Geometry was complicated if you don't follow the steps on solving it and analyze each questions!..Before I was really having a hard time on some topics in this lesson esp inequalities and solving 3 equations. But everything had change and went clear after Mr. K teach each every steps how to solve it!...I really enjoyed learning in class! hopefully this test will be great!and hopefully I'll do great as well. I hope I will use the right formula in right equations and solve them properly!..
good luck for tomorrow's test!!..
study hard!!.= ]
Reflection
Analytic geometry first I had trouble solving some problems but when Mr. K teach us a lot more and give more problems to solve I think I got some of it. This unit is not easy it takes time to know how to solve it. Well for me it is but for some of the class I think their good at solving things. Hope I can solve them right on our test tomorrow..MONDAY!..Hope you all have a nice weekend...see you all on monday.. Good Luck on test ClassMates^_^
Reflection..:>
Saturday, November 22, 2008
Reflection: Analytic geometry Test...
ahmm,, I think this unit is quite hard for me, especially when it comes to rational inequality but thanks to mr. K I finally understood how to solve it, so I'll do my best on our test. In this unit my favorite topic is the system of equations because I think it is much easier than inequalities. When solving inequalities I prefer to use number line instead of using graph because when I'm using graph it confuse me.. =)
Ok I think that's it...
GOOD LUCK EVERYONE on OUR TEST!!!
aja!! :)
Friday, November 21, 2008
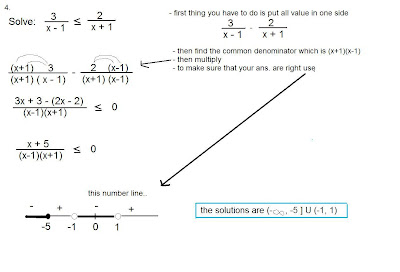
Hi...It's kim ur scribe 4 2day..... today Mr.k gave us the following equation...



Oh...Actually today Mr.K also introduced Geometry.......

 1.The sum of the angle of triangle is 180 degrees
1.The sum of the angle of triangle is 180 degrees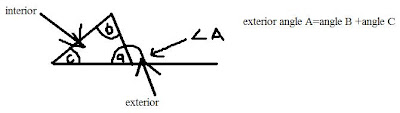
2.The measurement of an exterior angle to a triangle is equal to the sum of the interior opposite angle .
 3.Alternative angles are congruent
3.Alternative angles are congruentTransversal is the line that intersect the parallel line
The word congruent means equal..
For a long term memory just always remember the letter Z when your dealing with alternative angles.
 4.Corresponding angle are congruent
4.Corresponding angle are congruentFor a long term memory just always remember the letter F.,.....
 5.opposite angle are congruent ,remember the letter X......
5.opposite angle are congruent ,remember the letter X...... That's the different types of triangle that we are going to encounter in our Geometry unit.
That's the different types of triangle that we are going to encounter in our Geometry unit....why does triangle is equal to 180 degress...Proof
next scribe will be ...Niwatari-san
Thursday, November 20, 2008
Pre- Test on Analytic Geometry
Today in class we did our pre-test but before that, we work on Analytic Geometry #8
here's the question...
8. The total number of known moons around Saturn, Uranus, and Neptune is 43. The total number of moons around Saturn and Neptune is 9 more than the number of moons around Uranus. Saturn has 2 moons more than twice the number of moons around Neptune. Find the number of moons each planet has.
To solve this problem you have to do the following:
- first, you have to find the equation
- Then when you have the equation, set it up so it will be easy for you to solve it.
- Then when solving it, you can use elimination or substitution
here's the equations..
U = # of moons around Uranus
N = # of moons around Neptune
S + U + N = 43
S + N = U + 9
S = 2 + N
(click the images to make it big)

Wednesday, November 19, 2008
Analytic Geometry Review
z=3
Tuesday, November 18, 2008
Analytic Geometry
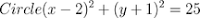
Y1=-2x+5
Y2=-1.2+5
After that we did some review questions and here is the first one that we have to find the centre and the radius of a circle.
- To find the centre, find the additive inverse of the X and Y. Which is -1,4. There fore the centre is (-1,4).
- To find the radius, square both side and you will find the that answer is the square root of 13.
2) The second Question was a little bit different than the first one because we have to find the distance between a point and equation of line. (3,4) to the line 2x-5y=7
after you plug the numbers into the equation you will find that the distance is
BOB Paul
The thing that I need help on is equations with three variables. We didn't go very in depth with this subject on class and I need more explaining on it.
Monday, November 17, 2008
Where Are We Wordle
This wordle was generated by the first 13 BOBs written tonight.
Tell me, what do you see?

Just a bit of help for Niwatori-san?
And im not quite sure about when you are given such an equation such as this one shown from quite a while back
http://www.slideshare.net/heviatar/pre-cal30-s-oct27-presentation. Im just not sure about the squaring the square-root. I know you square the other side also but then you end off with a radical and the variables that came along with it after isolating the variables.
Thanks Mr . K if what I asked gets cleared up so im not in mud anymore =p
Things i need help on ...
- Sayana
Welcome back, Mr. K!
- Circles
- Imaginary roots/Discriminants
- Quadratic Formulas
- Ambiguous Triangles
Thanks,
-Julius
Welcome Back Mr. K!
* The Ambiguous cases of triangles.
* Circles
* Radical and Rational Equations
Welcome back Mr. K!!
today is a fresh start for each of us! Mr. K just arrived and i know were all excited to see him:))
today we have an assembly which means we had a short class.
our today's class was divided into three points:
1. Reintroduction - which means going over our previous topic, the quadratic function, triginomentry (sin, cosine, tangent and ambiguous triangles), analytic geometry.
2. Blogs, Scribe Post, Digital Ethics - Mr. K mention that we need to blog every single day means that everyone should participate, because its also important that everyone knew what's going one in class and if someone is absent in our class they can go to blog and check what they missed. And its worth 5% of our class mark, so we better do it:D.
3. Where we at! - where on analytic geometry right now and were almost done with this topic and soon were going to write our pre-test and test.
Before the assembly Mr. K give us the homework which we have to blog and tell him if we need extra help with the previous lessons or topic, so he will have an idea where we are at. So we better do it because its our chance to review some stuff.
He also gave us our homework for tonight. We need to solve this equation
(x-2)squared+(y+1)squared=25 (equation of a circle)
2x+y=5 (equation of a line)
Mr. K said we need to find a points of intersection where the circle and the line intersect. the point is (2, -1), the 2x+y=5 we need to change it to a standard form of equation and substitute those points. These are just some clues to solve the given equation.
I think that's about it!..
Don't forget to do the homework and don't forget to arrive on class early tomorrow!!(so no lates)
Cheers:D
next blogger is NOHOM..:)
I'm thinking!
i need some help with these following topics..
-ambiguous triangles
-imaginary roots
-some trigonometry functions
-quadratic inequality
i think thats it..thank you...
Things I need help on.
- Imaginary roots
- Circle and a line questions/other line and a point questions
-Ambiguous triangles
so far that is all i can think off but a review of everything would be nice :D
Topics that I don't get...
here are the following topics that I still have to work on...
- circles and radius problems
- ambiguous triangles
- rational inequality
- absolute value inequality
Welcome back, Mr.K! :)
Here are the topics that I don't quite understand:
- Circles and Radius in Analytic Geometry
- Ambiguous Triangles
- Systems of Linear Equations in Three Variables
- Absolute Value Inequality
They're pretty much the same as the others -_-"
muddiest point
Absolute Values in Algebra
Circles and Radius Problems in Analytic Geometry
imaginary numbers... problems with those
unit Circle topic.
that's all i can think off -_-
What I'm Thinking.
Here are the things that I either need more practice on or get confused with:
☺ Absolute Values in Algebra
☺ Circles and Radius Problems in Analytic Geometry
☺ Adding-Subtracting Method in Systems of Linear Equations in Three Variables
I am struggling
- unit Circle topic.
- how you get the sin, cos & tan of the theta. I don't know how to deal with cos and tan. Like i cant solve this: cos^2(theta)=cos(theta) where 0degrees is greater than or equal to theta and less than or equal to 360. something like that. or this one: 3cos(theta)-1=-2cos(theta)
- ambigious triangle.
- As simple as getting the vertex. I am just weak with getting the vertex.
Things That I don't get
Here are the things that i don't get
- The Ambiguous cases of triangles.
- The equation of circle and working with the radius.
Digital Ethics
Here are a few videos that illustrate some of what I want you to think about:
Two teachers in the U.S.A. worked with their classes to come up with a list of guidelines for student bloggers.
One of them, Bud Hunt, has these suggestions, among others:
- Students using blogs are expected to treat blogspaces as classroom spaces. Speech that is inappropriate for class is not appropriate for our blog. While we encourage you to engage in debate and conversation with other bloggers, we also expect that you will conduct yourself in a manner reflective of a representative of this school.
- Never EVER EVER give out or record personal information on our blog. Our blog exists as a public space on the Internet. Don’t share anything that you don’t want the world to know. For your safety, be careful what you say, too. Don’t give out your phone number or home address. This is particularly important to remember if you have a personal online journal or blog elsewhere.
- Again, your blog is a public space. And if you put it on the Internet, odds are really good that it will stay on the Internet. Always. That means ten years from now when you are looking for a job, it might be possible for an employer to discover some really hateful and immature things you said when you were younger and more prone to foolish things. Be sure that anything you write you are proud of. It can come back to haunt you if you don’t.
- Never link to something you haven’t read. While it isn’t your job to police the Internet, when you link to something, you should make sure it is something that you really want to be associated with. If a link contains material that might be creepy or make some people uncomfortable, you should probably try a different source.
Another teacher, Steve Lazar, developed a set of guidelines in consultation with his students. You can read them here.
Look over the guidelines and add the ones you like in the comments section below this post; either from one of Steve's students or one of your own. I think Bud's suggestions are excellent. We'll be using the one's I highlighted above as a basis for how we will use our blog.
Cheers,
Mr. K.
Thursday, November 13, 2008
Today, Dr.A discussed the Quadratic,Absolute Value and Rational Inequalities.
Hmm...before that Dr.A explained the equation
 again,Camille perfectly explained it last day(similar thing)
again,Camille perfectly explained it last day(similar thing)if you want more info... or practice about Quadratic Inequalities ,just click the links below....
http://www.resources.mei.org.uk/sample/files/ascai2.htmlurces.mei.org.uk/sample/files/ascai2.html
http://www.algebra-online.com/quadratic-inequalities-1.htm
lets proceed to the critical numbers (where the function is undefined)....Rational Inequalities
ex..
x-1/(x-2)(x+3)<>
How many critical numbers are there in that equation?
Ans..
3 critical numbers (1,2,-3)
After we identified the Critical numbers were now ready to Graph it on the number line...

Decide which intervals include numbers that make x-1/(x-2)(x+3) negative by substituting any number .......
http://www.purplemath.com/modules/ineqrtnl.htm
let's try -4
just subtitute it to the equation x-1/(x-2)(x+3)
-4-1/(-4-2)(-4+3)===-5/6(negative)
try 0.....(positive)
try 3(positive)
the only number that satisfy the given inequality (first one) .....therfore the answer is...
(-infinity,-3),(1,2)
http://www.purplemath.com/modules/ineqrtnl.htm
Absolute value inequalities
lets solve this equation:

/x/<3
we are looking for those real numbers x whose distance from the origin is less than 3 units.
(-3,0] [0,3)
Wednesday, November 12, 2008
Linear Inequalities / Quadratic Inequalities
first off we hand in our homework due today!Ex 27 #11
=The sum of two numbers is 181. Three times the larger plus twice the smaller equals 459. Find the numbers
1. we need to set up the equation
x + y = 181
3x+2y=459
2. eliminate by multiplying x + y = 181
2(x + y)=2(181)
2x+2y=362
3. subtract
3x+2y=459
-2x+2y=362
so you'll get x = 97
4. substitute the x=97 to the equation 2x+2y=362 and find y
2(97)+2y=362
194 + 2y=362
2y=362-194
2y=168
y=84
1. we were given an example
x+y>6
2x+2y<5>
"and" means intersection
=we have to look for x and y plane where both equations are true.
the red broken line represents the 1st equation.
the black broken line represents the 2nd equation.
if we were to check the intersection of the points we need to find a points that satisfy the 2 equation.
(0,0) is the easiest point to chec
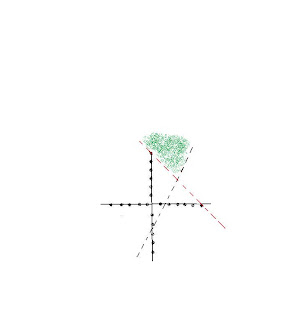 k if the line is not touching it!
k if the line is not touching it!so if we substitute that in the solution we will get:
0+0>6 that's true
2(0)+2(0)<5>the shaded part represents the intersection of the 2 equation.
*remember that ><>/\<>and included*
"or" means union
=we have to find
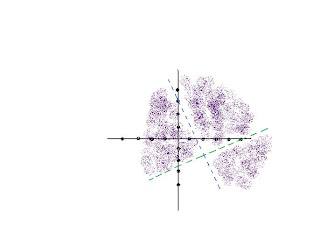 solution that satisfy 1 of the equation
solution that satisfy 1 of the equationx-2y<5>3
(again this line will be excluded and will be broken line)
the green line represents the 1st equation.
the blue line represents the 2nd equation.
we need to find each quadrant were one of the points satisfy one equation.
we also need to check each quadrant. we use the points (1,-5) where only one of the equation was satisfied.
we are finished on this topic. Now were moving on to the new one, its all about Quadratic Inequalities.
Speaking of quadratic, what image do you think will be using??the answer is the parabola.
equation will be *y=axsquared+bx+c*
1st step is to graph:
 this is a general parabola, we have to take a point inside and outside the parabola so we know which part should be shaded.
this is a general parabola, we have to take a point inside and outside the parabola so we know which part should be shaded.we are given an example:
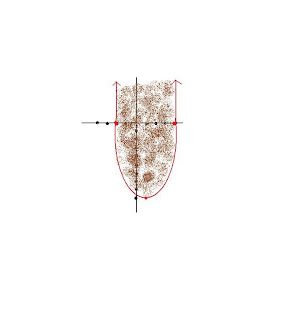 y>/x(squared)-2x-8
y>/x(squared)-2x-8-we have to find the vertex
b/2a=-2/2=-1
x=1
-then substiture
y=1-2-8
y=-9
so the vertex will be (1,-9)
then we need to find the intercepts
x(squared)-2x-8
(x+4)(x-2)
intercepts are (4,-2)
then we need to find a point inside and
outside of the parabola. (0,0) for inside, and (5,0) for the outside.

check:
0>/0-8(inside)
5>/5-8(outside)
next example is x(squared)-2x-8>/0
we use solid circle because the points are included, we use this in set notations.
*the blue line represents the outside points. [-2,-infinity] and [4,infinity].
*the maroon line represents the inside points, points between -2 to 4.
In this case we only have one dimension (x-axis) so you can drop the y-axis. We don't have to worry about it.
Again we always have to check if were right, we have to find a point that satisfy the equation.
(0,0) can't be the right point because if we substitute it we'll get 0-0-8>/0. Its wrong!
(5,0) we'll get 5+10-8>/0. Its right!
(6,0) we'll get 36-12-8>/0. Its right too!
So either one of the two points can be use to satisfy the equation but not (0,0)
____________________________________________________________________
Sorry because I'm not sure how to do the uppercase of 2 so i put squared!
The shaded part represents the intersection.
Oh don't forget we have homework to do! Exercise 28 # 1-3
hope you did learn something on my blog!!..good luck to everyone!!:))
cheers!!!
the next scribe will be Kim C.:D..
Linear Inequalities.
teacher said, we could represent each linear inequalities by these representation:
 this means that > with out the underscore at the bottom that 6 is included in the solution
this means that > with out the underscore at the bottom that 6 is included in the solutionand for y >(with the underscore at the bottom) 6 means that it is not part of the solution
 she gave a couple of examples like this..
she gave a couple of examples like this..

normally its always easy to figure out the right region when you use (0,0)
last example the teacher gave us was this one:
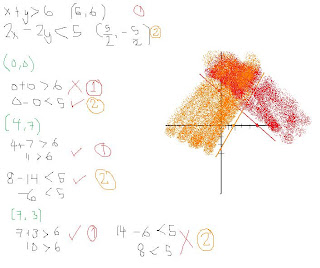 the intersection of these two inequalities is where they both intersect in this case they intersect at the region where you see both colours are present.
the intersection of these two inequalities is where they both intersect in this case they intersect at the region where you see both colours are present.That's it. next scribe is Camille : P
Sunday, November 9, 2008
Circle Hyperbola
Sorry for the late post, but here's what we did on Friday.
First off, we went through the homework that were given on Thursday.
w + l + h = 80 cm
Length=10cm less than twice the sum of width and height and twice the width exceeds the height by 6 cm. Find the width, length and height of the box.
~We didn't go over the procedure on how to solve this problem, but the answers were:
h = 18cm, w = 12 cm, l = 50 cm
Then there was the question from the book (Ex. 25 #1) Letter "c" was done by Ramina on the white board. For those who didn't get to copy the procedure, here it is...
1. a) 3x-4y+5z=2
4x+5y-3z=-5
5x-3y+2z=-11
(3) 3x-4y+5z=2 (3)
(5) 4x+5y-3z=-5 (5)
9x-12y-15z=6
+ 20x+25y-15z=-25
ˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉ
29x+13y=-19
(2) 4x+5y-3z=-5 (2)
(3) 5x-3y+2z=-11 (3)
8x+10y-6z=-10
+ 15x-9y+6z=-33
ˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉ
23x+y=-43
29x+13y=-19
(13) 23x+y=-43 (13)
29x+13y=-19
+ 229x+13y=-559
ˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉ
-270x = 540
ˉˉˉˉˉˉ ˉˉˉˉˉ
-270 -270
x = -2
29x+13y=-19
29(-2)+13y=-19
-58+13y=-19
13y=58-19
13y=39
ˉˉˉ ˉˉˉ
13 13
y = 3
3x-4y+5z=2
(3)(-2)-4(3)+5z=2
-6-12+5z=2
-18+5z=2
5z=18+2
5z = 20
ˉˉˉ ˉˉˉ
5 5
z = 4
After this, we talked about a little something new called Circle Hyperbola.
It looks like this ...
A Circle Hyperbola can only have 0, 1, or 2 intercepts and no more than that. We can find the intercept by putting the equation on our calculator OR solve it algebraically. We did some examples as a practice on finding the intercepts of Circle Hyperbola.
► y=x-1
y=x²-6x+9
x-1=x²-6x+9
-10=x²-7x
x²-7x+10=0
(x-5) (x-2)
x=5 x=2
y=4 y=1
another example was...
►x²-y²=5
xy+6=0
y²=x²-5 → y= √x²-5 (#1)
y=-6/x (#2)
-6/x=√x²-5
(-6/x)² = (√x²-5)²
36/x² = x²-5
x^4-5x²=36 (substitute x^4 to u=x²)
u²-5u-36=0
(u-9) (u=4)
u=9, -4
x²=9, -4
x=±3
x=3 , y=-2
x=-3 , y=2
After doing these examples, there were homework that were assigned for us to do. Exercise 26 (# 1-5) Also, don't forget to hand in your bonus mark homework sheets before Dr. Eviatar leaves!
-
-
-
Next Scribe ... Jamie
Thursday, November 6, 2008
Chae: le six novembre 2008
I decided to do the blog today since I happened to check on the blog and didn't see an update. I hope Dr.Eviatar doesn't mind if I scribe here with "no permission" :)
Well, today we had to hand in #6 of Exercise 24 from the book. There were some volunteers who put the answer for it on the board. I didn't quite know how to do it, so I didn't volunteer.
Here are the answers for #6 a.)&b.)
a.)
3x + 2y = 4 -->equation [1]
x - y = 3 -->equation [2]
Multiply the equation [2] by 3 like this:
3(x - y - 3) = 0
=> 3x - 3y - 9 = 0
Then you subtract the new equation from the first [1] equation:
3x + 2y - 4 = 0
- 3x - 3y - 9 = 0
5y + 5
Find the value of y:
5y = -5
=> y = -1
Substitute the value of y in the equation [1] to find the value of x:
3x + 2(-1) = 4
3x - 2 = 4
3x = 6
x = 2
Answer is: (2,-1)
b.)
2x + 3y = 48
3x + 2y = 42
Same process, but this time you multiply both equations to get rid of y:
2(2x + 3y =48)
=> 4x + 6y = 96
3(3x + 2y = 42)
=> 9x + 6y = 126
Addition-Subtraction Method:
4x + 6y = 96
- 9x + 6y = 126
-5x = -30
Value of x:
-5x = -30
=> x = 6
Substitute the value of x to get the value of y:
2(6) + 3y = 48
12 + 3y =48
3y =36
y = 12
Answer is: (6,12)
After that, we started a new topic. It was sort of the same as our previous topic (Systems of Linear Equations in Two Variables), but this time it is for THREE variables. I'm still in the process of understanding it, so pardon my explanations. Well, all I have right now are some notes from the board (-_-"). It was so much better when we can just look at the slides again in the blog for information.
But anyway, here are the notes:
Independent - 1 Solution (all 3 equations intersect)
Dependent - Infinite solutions -> concide
-> common line
Inconsistent - No solutions
The graph for the "Ordered Triple" example (3,3,3)
The graph was sort of hard to draw, and to understand. As a matter of fact, I don't really get how you draw the points in it. That's why we're not really asked to draw the graph.
Example of how to solve equations with THREE variables:
x + y - z = 2 --> [Equation 1]
x - 2y + 2 = -1 --> [Equation 2]
3x + y - 2z = 4 --> [Equation 3]
Steps:
1st:
[Equation 1] + [ Equation 2]
=> 2x - y = 1 --> [Equation 4]
2nd:
2 * [Equation 2]
=> 2x - 4y + 2z = -2 --> [Equation 5]
3rd:
Equation 3 + Equation 5
=> 5x - 3y = 2 --> [Equation 6]
4th:
3 * [Equation 4]
=> 6x - 3y = 3 --> [Equation 7]
5th:
[Equation 6] - [Equation 7]
=> x=1
Substitute x=1 into [Equation 4]:
=> 2 - y = 1
=> y = 1
Substitute x=1 and y=1 into [Equation 1]:
=> 1 + 1 - z = 2
=> z = 0
Answer to the equations: (1,1,0)
Well, that's all the notes that was for today. Things for homework are Exercise 25 #1, and the problem she wrote on the board.
In case you weren't in class or didn't get to write it down, here is the problem (Parts of it are already summarized/put into an equation by Dr.Eviatar):
w + l + h = 80cm
Length is 10cm less than twice the sum of width and height and twice the width exceeds the height by 6cm. Find the width, length, and height of the box.
l = 2 (w + h) - 10
2w = h + 6
That's practically what we did for class today. I hope I helped in the new topic in some way. I'm not going to pick who's going to be the next scribe since I sort of just barged in the blog to put what we did today [kind of saying that I scribed with "no permission", haha.] I have to do the homework myself. I'll at least "try" to do it (-_-") I'm still trying to understand the given problem.
Till next time my fellow classmates,
Charizze ^-^
Sunday, November 2, 2008
Digital Ethics
http://pc40sw08.blogspot.com/2008/02/digital-ethics.html
Cheers, Dr. Eviatar.