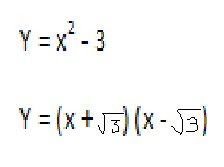Friday, January 23, 2009
Thursday, January 22, 2009
A hole in the graph
Today in class, we continued doing the unfinished example from yesterday's class. The first thing we did was Mr. k showed us the video of a real "Plug Hole" because it is related to our topic today. Here's what he showed us "Plug Hole (short version)" "Plug Hole (long version)" Feel free to watch it..
Anyways here are the examples we did...




next scribe is Ashley
Wednesday, January 21, 2009
More about Rational Functions
Sorry for the delay I almost forgot that I have to scribe for today's class.
Today, Mr.K reviewed about the Graphing Function that we did for yesterday's class.
Remember: The seven steps of doing the Graphing Function;
6th step: Sign Analysis
Function mix with Niwatori-san XD
Itz function time last unit for this curriculum but not the last for your school year!
T_T
Oh stop crying about it letz go on with some learning!
Well following with the Synthetic division as well as the RATIONAL ROOTS THEOREM . . .
we can get sketching a graph well worth the time to look at. =p
Please follow these steps as followed to sketch the graph!
Step 1: Find your Y-intercept by letting variable X become zero like this
e.g . . . . . (x=0)
Good job you're smart!
Step 2: Find all rational roots possible while reminded to wiping out the copied numbers
(Use the rational roots theorem if needed)
Okay next step!
Step 3: Determine the sign of the function by looking at the different ways the X intercepts are hitting the X-axis such as -2 hitting at X and another hitting +2 see different spots!
Final Step! *Was going to do a drum beat but I let the drum just roll away* Step 4: Sketch the Graph! XP (what did you expect Oprah Winfrey forget it!)
Of course this is done after you get show the work so these following diagrams will show you how:
1st use Synthetic division mind yourself this is to find Polynomial Functions I will touch with Rational Functions in the next one!
 Ok, you got the roots time to graph it with the roots acquired!
Ok, you got the roots time to graph it with the roots acquired!Use the equation and get the Y-intercept by letting the X's in the equation F(x)=4X^3+3X^2+4X+5
so...
Y = 4(0)^3+3(0)^2+4(0)+5
= 5
After doing this you can make a number line including all the Roots/X-intercepts depending on the context used in this case it's roots for the number line
Sketching Rational Functions is just a bit of an extra step! All that is different is that you need to look for vertical asymptotes.
Asymptotes are lines on a graph not meant to be there but they are there to show that certain part of the Cartesian plain is not allowed to have a(n) point to touch the line. If the point does touch then there is something wrong with the graph.
*Be careful to not mistake the Asymptote as part of the graph itself!*
Oh yes, quick reminder you have to find both horizontal and vertical Asymptotes not just the vertical.
 Ok... that was to get the horizontal asymptote but to get the vertical asymptote you just need the root of the denominator!
Ok... that was to get the horizontal asymptote but to get the vertical asymptote you just need the root of the denominator!*****Please notice!!! that not all the time will there be an asymptote!!! So no need to worry if there isn't one present!!!****
Niwatori-san signing off I'll see you all in the next year. Have fun next Pre-cal class and hopes to always to feel happy as well obliged to use your own voice to help out your peers.
"A little voice from you could change a lot from the many in silent"
-By: Niwatori-san- GAMBETE FOLKS!
> . < So sorry people I forgot to scribe the past two times but yeah I had work and even though that be a bad excuse to skip scribing I'm still sorry!
Tuesday, January 20, 2009
Graphing Rational Functions
Example:
Step 1: Find the y-intercept by letting x=0.

Step 2: Factor everything, which in this case it's already factored.
Step 3: Find the roots of the function by finding the roots of the numerator.
This one has NO ROOTS.
Step 4: Find the vertical asymptotes by finding the roots of the denominator.
V.A. → x=2
Step 5: Find the horizontal asymptotes by dividing each term in the function by highest power of x, and take the limit as x goes infinity.

H.A. → y=0
Step 6: Determine the sign of the function over the intervals defined by the roots (step 3) and vertical asymptotes (step 4).
Step 7: Sketch the graph.
This is not the the exact graph, but it gives us idea on how the graph would look like.
We did another example on graphing rational functions, but it's pretty much the exact same thing on how we solve it. The only thing that changed was the graph (we can see this on the slides that Mr. K post everyday).
Homework: Go back to the Exercise that was assigned yesterday and and do the graphing rational functions part of it. Also, don't forget to start on doing the last exercise in the book that covers all the units that we did in Pre-Cal.
Next scribe is Larlyn
Monday, January 19, 2009
Friday, January 16, 2009
Thursday, January 15, 2009
Remainder Theorem and The Rational Roots Theorem
After that, we learned how to find the missing coefficient in a polynomial if we already know what the remainder is. Here's how you would do this:
Let's say you have the question:
The first thing you want to do is write it out in a way that is easy to understand:
Then you plug the root of the denominator into the function:
Since we already know the remainder we can rewrite it this way:
Now all we do is isolate K with a little algebra, and solve it:
And there you have it!
Near the end of the class we managed to quickly learn the Rational Roots Theorem. This theorem allows us to find any rational roots of a polynomial function. Here's an example:
So you're given the equation:
The first thing to do is the find all the possible positive and negative factors of the constant term:
Now we find all the positive factors of the leading coefficient:
We then list all the possible rational roots, eliminating any duplicates:
We can then test out these roots by using synthetic division and the factor theorem to turn the function into a quadratic (Remember: If the remainder is 0, then it is a root):
This then gives you:
Now you just factor the equation and find the roots:
And there you have it! That's about all we did for today, tomorrow's scribe will be...Niwatori-san
Wednesday, January 14, 2009
Tuesday, January 13, 2009
January 12
Anyways, we did the rational roots theorem and the synthetic divison.
The following questions for the rational roots theorem were:
Find each of the following and their domains: fOg, gOf, fOf, gOg.
f(x) = 2x+3, g(x) = 4x-1
fOg(x) = f(g(x))
They're the same equation. What fOg(x) means is that g is fed up inside of f which is the same as f(g(x)). Same goes for the other functions gOf = g(f(x)), fOf = f(f(x)), gOg = g(g(x)).
Now lets try fOg(x):
f(g(x)) = 2(4x-1)+3
= 8x-2+3
= 8x+1
Another function: f(x) = √x-1, g(x) = x2
fOg(x) = f(g(x))
= √x2-1
We cant simplify this any longer, so we leave it at that. Lets move on to...
Synthetic Division.
I hate dividing because it was too long. It eats up half of your paper when you do division but Mr. K showed us the easier way to divide.
For example:

The 7 on the left side is the root of x - 7. The 2 was brought down. Now 7 * 2 = 14, we put the 14 under 6. Then 14 + 6 = 20. We are now adding instead of subtracting compared to the long division. Subtraction can lead to different answers. We then multiply 7 * 20 = 140. We put the 140 on the next, under -40. Now we can add (-40) + 140 = 100. So we multiply 700 by 100 and we get 700, we add 700 to 1 and we get 701.
Now we have 2 20 100 701. We start on the very right side. We have 701 which is a remainder. So we put that as 701/x-7. Next up is 100. After the remainded we have the constant. So 100 is our constant. Next up is 20 and it becomes 20x and 2 becomes 2x2 . So we have 2x2 + 20x + 100 + 701/x-7.
Monday, January 12, 2009
Sunday, January 11, 2009
function inverse and composition
If we can compose a function. We must also be able to decompose it.for function decomposition we have to understand the "inner function" and the "Outer function"
for example if we have f(x)= 1-x^2 in order to decompose the function F(x)= x^2 Inner function
g(x)= x+1 Outer function
f(x)=1/x^3
F(x)= x^3 Inner function
g(x)=1/x Outer function
for more information about the function composition visit
http://www.purplemath.com/modules/fcncomp.htm
http://oregonstate.edu/instruct/mth251/cq/FieldGuide/composition/lesson.html
http://www.youtube.com/watch?v=S4AEZElTPDo
After the function decomposition we talked about the function of type
many to one function.
Different from one to one function where every one element of the input or the domain correspond to one element of the output or range. A many to one function is a function where every one element of the input domain correspond to more than one element of the output or range.

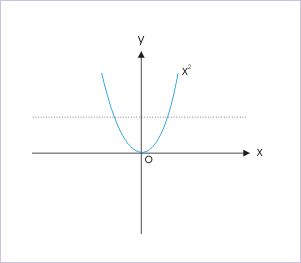 many to one function
many to one function
We have to remember that
Input = Domain which is a set of all the first elements of the ordered pairs of a function
Output = Range which is a set of all the second elements of the ordered pairs of a function.
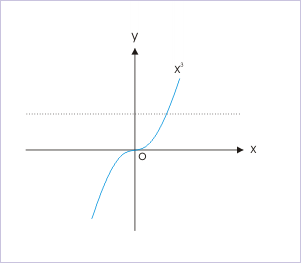 one to one function
one to one functionOne-to-one function are special because they are invertible
If a horizontal line intersects a function's graph. more than once, then the function is not one-to-one.
Passes the test

Fail the test
if ƒ is a function from A to B then an inverse function for ƒ is a function in the opposite direction, if an input x into the function ƒ produces an output y, then inputting y into the inverse function ƒ–(read f inverse) the inverse of a one-to-one function is obtained by switching the role of x and y.ƒ– the inverse of a one-to-one function is obtained by switching the role of x and y.

the inverse of a function is defined by
General procedure for finding the inverse of a function:
- Interchange the variables - First, we will exchange the variables. We do this because we want to find the function that goes the other way, by mapping the old range onto the old domain. So our new equation is x=2y-5.
- Solve for y -The rest is simply solving for the new y, which gives us:
2y-5 = x
2y = x+5
y = (x+5)/2
Hence, y-1(x) = (x+5)/2
Friday, January 9, 2009
Thursday, January 8, 2009
Functions
We can express functions in ways such as:-
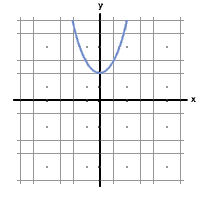
2. Graphs:- For example this is a graph of the equation f(x)=x^2+2.
We have also talked about relations. Relation is a set of order pairs.
Types of relation functions
1. One-to-one Relation:- this relation is a function because only one element of set A is corresponding another element in set B.

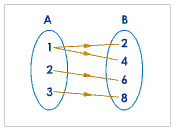
2. One-to-many Relation:- this is not an a function because the element 1 from set is corresponding to 2,4 in set B.
3. Many-to-one Relation:- 3 elements from set A are corresponding to the element 4 in set B which is many to one.

We have also talked about the vertical line test. It is a vertical line that touches the graph only once.
For example this graph is a Function because it touches the vertical line test once.
Sources :- http://www.tutorvista.com/content/math/algebra/function/function.php
http://www.purplemath.com/modules/fcns.htm
Next Scribe :- Ale ...
Wednesday, January 7, 2009
reflection
Tuesday, January 6, 2009
REFLECTION
tomorrow will be our test on Logic.. In this unit I'm pretty sure that I can answer them on the test....although I don't get a chance to review this morning with all of the class, because I got really sick and won't be able to go to class.. I think I'm going to do fine...anyways.. I think this unit is okay and I think I can handle them...LOL!!...;) anyways...good luck to all of you...^_^
Reflection .
Good Luck!
Reflection!
Tomorrow is the test, and I am quite ready but the only thing that I don't understand is the difference between inductive and deductive reasoning.
Reflection...
For this unit, I can say that it was quite easy. But I still have troubles on proving by contradiction (the indirect and direct reasoning thingy). Overall, I think that I am capable of answering the questions on the test. Yet, I am still quite nervous because I don't guarantee a perfect mark on it since I found some part of the unit a little difficult. I hope that everyone would do well on the test tomorrow! ^-^
-CharChar
Reflection
To be honest..
I think I'm still not confident for tomorrow's test because I still have some topics that I don't get and when when I look at it I get confused :( . Such as determining the truth or false in Conditional Statement, Contradiction and Counter example. But I hope I'll be able to understand it tonight :)
See yah all tomorrow... GOOD LUCK!!!
Reflection
Good luck to all !
Reflection
I just want to remind everyone that its our LOGIC TEST tomorrow!!
I'm kinda nervous about the test tomorrow because I have some difficulties understanding some topics.
I don't get these following topics:
=counterexample
=proof of contradiction (esp solving problems using graphs)
And that's everything:)..I hope everyone will do great on the test tomorrow!good luck!!
Review Class
 Some of the questons you will see on the sheet, we've already went over so it shouldn't be to hard to answer. It was also said that in the beginning of the class that the questions on the sheet were taken from past tests. So what you see on that sheet is basically a test in itself. So its safe to say, the questions seen are identical on what you will see on tomorrow's test.
Some of the questons you will see on the sheet, we've already went over so it shouldn't be to hard to answer. It was also said that in the beginning of the class that the questions on the sheet were taken from past tests. So what you see on that sheet is basically a test in itself. So its safe to say, the questions seen are identical on what you will see on tomorrow's test.As for question 9, you will need to make a chart to solve. I've made a chart for those of you who need it As you may have noticed, there is a question mark in place of one of the points. I have yet to figure out what that value is. Most likely you will need to go trough the problem to be able to find the value.
As you may have noticed, there is a question mark in place of one of the points. I have yet to figure out what that value is. Most likely you will need to go trough the problem to be able to find the value.
Thats it for today's class.
Remember: Test Tomorrow
Good luck and study hard !
Next Scribe: Nohom
Monday, January 5, 2009
It's 2009! :D Scribe post for January 05, 2009
(a) The statement is true but its converse is false.
(b) The statement is false but its converse is true.
(c) Both the statement and its converse are false.
(d) Both the statement and its converse are true.
I think I explained them as well as I could. Tomorrow, we will have time to review Logic with the class once more. Homework for today was to try to prove if  is rational or not. Look at the slide that was on December 19 for the explanation on
is rational or not. Look at the slide that was on December 19 for the explanation on  because it is similar. Also, we have to finish other unanswered exercises that we were assigned including Exercise 50.
because it is similar. Also, we have to finish other unanswered exercises that we were assigned including Exercise 50.
That is all for today! ^-^
The next scribe will be Randall :]
- CharChar